Б.И. Бахтин, кандидат технических наук, 3-й дан IFK,

Д.С. Шапошников, инженер, 4-й дан IFK

 

Многие из приверженцев восточных единоборств после какой-то стадии успешных тренировок решаются проверить силу своих ударов в тамэсивари. Почти каждый из них, оказавшись один на один с предметом, который необходимо вдребезги разнести, оказывается в какой-то момент времени перед мучительной дилеммой, подобно Гамлету из пьесы У.Шекспира – «бить или не бить». Выбор становиться особенно ответственным для участника соревнований по тамэсивари – стремление к высокому результату может завершиться тяжелой травмой. Реалии таковы, что на сегодняшний день единственная проторенная дорога поиска предела собственной ударной мощности основана на эмпирике – опытном пути проб и ошибок. Сочетание слов – путь ошибок – означает в нашем случае неизбежность неудачных попыток выполнения тамэсивари с высокой вероятностью получения травм ударных конечностей (ударных звеньев тела).

Существует ли возможность снизить травматизм с привлечением альтернативного подхода к ответу на поставленный выше вопрос. Вспоминаются слова из популярной когда-то спортивной песни: «нужны в футболе не только ноги, нужна в футболе, между прочим, голова». Если использовать голову не только как грозное ударное звено, но и как аналитический аппарат, то можно попытаться оценить потенциальные разрушительные возможности удара с позиций теории прочности (курса сопромата – сопротивления материалов).

При аналитическом подходе к решению задачи («бить или не бить») ее можно разделить на ряд этапов или условий, выполнение которых обеспечивает достижение поставленной цели – сокрушение объекта тамэсивари без повреждения конечностей:

1. Восточные единоборства относятся к области боевых искусств и здесь уместно использование военной терминологии. Всякая военная операция должна начинаться с разведки. Прежде чем обрушить удар на разбиваемый предмет, следует изучить, с помощью расчета или эксперимента, его прочностные характеристики – как минимум, величину усилия Fр, воздействие которого приводит к разрушению объекта, и значение энергии Wр (работы), которую необходимо для этого затратить.

2. Следующее условие связано с потенциальной возможностью исполнителя тамэсивари обеспечить при ударе необходимые уровни усилий (амплитуды силы) и энергии. Зная массу ударного звена (например, масса кисти и предплечья составляет примерно 2,2% от массы тела) и его скорость (ориентировочный возможный диапазон 5-10 м/с), можно рассчитать кинетическую энергию, развиваемую звеном, и сравнить ее с величиной Wр. Для оценки амплитуды силы при ударе необходимо знать путь торможения ударного звена (деформацию предмета до его разрушения). Чтобы потенциальные возможности сокрушительного удара были реализованы, необходимо провести цикл специальных тренировок для освоения оптимальной техники удара, позволяющей объединить импульсы движущихся звеньев тела в один мощный общий импульс ударного звена.

3. Выполнение первых двух условий не избавляет от возможности получения травм при выполнении удара, если ударные звенья тела не прошли специальную подготовку. Контактные поверхности ударных конечностей, их связки, сухожилия, кости, суставы, мышечные группы должны быть натренированы к перенесению экстремальных импульсных нагрузок по известным в восточных единоборствах методикам.

4. Последнее условие заключается в твердой (безусловной) психологической установке (самокодировании) на успешное достижение цели, основанной на позитивных результатах продвижения по предыдущим этапам. Уверенность в успехе должна быть абсолютной, малейшее сомнение может послужить спусковым крючком для инстинкта самосохранения с неконтролируемым затормаживанием ударного звена в последнее мгновение удара и последующими неприятными последствиями.

Задачи настоящей статьи были ограничены рамками первого из перечисленных выше этапов. Поставленная цель состояла в определении требуемых параметров разрушающего удара на основе теоретического или экспериментального подхода. Как показало ознакомление с доступной литературой, в которой обсуждаются проблемы тамэсивари, прочностные характеристики разбиваемых предметов практически в этих работах не представлены.

Проще рассмотреть параметры разрушения объекта сначала при статическом нагружении, а затем – при динамическом. В качестве примера разрушаемого объекта рассмотрим деревянную доску длиной L, шириной b и толщиной h.

1.1. Статическое нагружение досок. 

При выведении формулы для расчета статической нагрузки, которая может привести к разрушению доски, используется правило баланса (равновесия) сил и моментов, действующих на всю доску или ее отдельные части (метод мысленных сечений). Схема доски, опирающейся на две опорные подставки, показана на рис.1. Характерная особенность структуры разбиваемых досок состоит в ориентации волокон древесины – они расположены вдоль ширины доски, как показано на схеме. Такая ориентация снижает разрушающую нагрузку почти на порядок величины по сравнению со случаем расположения волокон вдоль длины доски. 

Подставки можно мысленно убрать, заменив их для сохранения баланса сил реакциями опоры R, как показано на рис.2. 

Из условия баланса сил: 

F = 2R или R = 1/2F      (1) 

Воздействие сил F и R приводит к появлению поперечных (вертикальных) сил сдвига Q в поперечных сечениях доски (постоянных и равных R во всех сечениях), а также к изгибу доски со смещением вниз ее центральной части на величину δ. 

Верхняя часть доски оказывается при этом в зоне действия сжимающих сил, нижняя – в зоне сил растяжения. В средней (нейтральной) плоскости (пунктирная линия) силы растяжения-сжатия равны нулю. Однако, вдоль этой плоскости могут достигать максимального значения касательные силы, возникающие как раз из-за того, что часть доски выше нейтральной плоскости сжимается, а ниже нейтральной плоскости – растягивается.

При относительно большом удлинении доски (L>b, L»h) наиболее высокие внутренние напряжения (силы, приходящиеся на единицу площади сечения), возникают в среднем поперечном сечении в результате изгиба доски с появлением нормальных к поперечному сечению сил растяжения-сжатия. В связи с этим, при расчете прочности досок рассматривают, в первую очередь, напряжения растяжения-сжатия. В среднем (центральном) поперечном сечении силы F и Q не создают момента сил (плечи сил равны нулю), а сила R создает на плече L/2 момент, равный 

Мr = R(L/2)     (2) 

Следует отметить, что на рис.2 для упрощения дальнейших выкладок реакции опоры условно расположены на краях доски (на расстоянии L друг от друга). При более строгом подходе к постановке задачи нужно иметь в виду, что расстояние между силами R равно расстоянию между опорными подставками Lо (рис.1), которое немного меньше L (на 10-20 мм). 

Момент от силы R уравновешивается моментом Мσ, создаваемым внутренними силами растяжения-сжатия в поперечном сечении доски (рис.3). 

На схеме рис.3 правая половина доски мысленно удалена, а ее влияние на левую половину представлено в виде напряжений растяжения-сжатия σ, достигающих максимального значения σмах в зоне верхней и нижней плоскости доски. Силы F и Q на схеме не показаны, так как они, как уже говорилось выше, не создают момента относительно главной центральной оси, проходящей через линию пересечения поперечной плоскости с нейтральной плоскостью. Если каждое из напряжений, действующих на локальную единичную площадку поперечного сечения, умножить на высоту расположения этой площадки (расстояние до нейтральной плоскости), то получим локальный момент от этого напряжения относительно главной центральной оси. Просуммировав локальные моменты по всей площади поперечного сечения, придем к значению момента от напряжений (сил) растяжения-сжатия Мσ. 

Из условия Мσ = Мr = FL/4 можно найти связь между силой F и максимальным напряжением σмах. Не злоупотребляя терпением читателей, мужественно добравшихся до этого места статьи, приведем искомую зависимость в окончательном виде: 

F = (2/3)(bh2/L) σмах     (3) 

Небезинтересно отметить, что зависимость прилагаемой силы от толщины доски носит квадратичный характер. Это означает, например, что при возрастании толщины доски в два раза силу F надо увеличить в четыре раза, чтобы обеспечить одинаковое значение максимального напряжения растяжения-сжатия. Снижение толщины доски в два раза уменьшает требуемую силу в четыре раза в полном соответствии с народной мудростью – «где тонко, там и рвется».

Как видно из формулы (3), максимальное напряжение возрастает пропорционально величине прикладываемой силы. Когда значение максимального напряжения σмах достигнет предела прочности древесины σп, начнется процесс разрушения доски. Предел прочности древесины на растяжение, как правило, выше, чем предел прочности на сжатие (в отличие от металлов и сплавов), поэтому первая стадия разрушения (смятие волокон) начнется в середине верхней части доски. Это приведет к общему ослаблению прочности доски в поперечном сечении с последующим появлением трещины уже в нижней части доски и дальнейшим ее окончательным растрескиванием.

Аналогичная картина наблюдается при раскалывании блока из нескольких досок (фотография на рис.4).

Подставив в уравнение (3) предел прочности σп на сжатие вместо σмах, получим формулу для расчета статической нагрузки, при которой начинается процесс разрушения доски: 

Fп = (2/3)(bh2/L) σп     (4) 

Если известна диаграмма деформации (прогиба) доски под воздействием нагрузки, то можно определить величину работы (энергии), затрачиваемой на разрушение. Эту диаграмму можно упрощенно представить в виде двух характерных участков (рис.5). На первом участке величина упругого прогиба доски δ линейно связана со значением действующей нагрузки F. На этом участке действует закон Гука, в соответствии с которым деформация материала пропорциональна создаваемому в нем напряжению. Известна формула для расчета прогиба доски на этом участке в зависимости от прикладываемой силы /3/:

δ = FL3/4Ebh3     (5) 

где Е – модуль упругости (модуль Юнга) древесины при ее растяжении-сжатии поперек волокон. 

Для первого участка легко рассчитать энергию (работу), затрачиваемую на упругий изгиб доски (геометрически – площадь под диаграммой): 

W1 = (1/2) Fп δп     (6)

Рис.4. Раскалывание блока из 5 досок

1-участок упругих деформаций, 2-участок разрушения. 

где δп – предельное значение прогиба доски, при котором перестает действовать закон Гука и начинаются необратимые процессы разрушения доски (δп можно рассчитать по формуле (4) приняв F = Fп ).

Эти процессы (второй участок деформации доски) реально происходят при относительно небольшом увеличении нагрузки. Второй участок заканчивается при появлении трещины в нижней части доски – в этот момент максимальная нагрузка достигает Fр, а максимальный прогиб соответствует величине δр. Для случая растяжения-сжатия древесины поперек волокон отношение Fр/ Fп можно принять равным 1,2 (при растяжении-сжатии вдоль волокон это отношение может достигать 1,3-1,5 и более). Средняя нагрузка на втором участке будет тогда равна Fср =1,1Fп. Величина энергии, затрачиваемой непосредственно на необратимые процессы разрушения:

W2 = 1,1Fп(δр - δп)     (7)

Если максимальный прогиб представить в виде δр = kδ δп, где kδ – коэффициент относительной деформации, определяемый опытным или расчетным путем, тогда уравнение (7) можно записать в форме

W2 = 1,1Fп δп (kδ – 1)     (7а)

Суммарная энергия, необходимая для разрушения доски 

Wp = W1 + W2 = 1,1Fп δп (kδ – 0,54)     (8)

К сожалению, попытки непосредственного использования представленных формул (4)-(8) наталкиваются на большие трудности. При создании строительных деревянных конструкций, работающих на изгиб (такие конструкции называются балками), не используют несущих элементов, в которых напряжения действуют поперек волокон, как это происходит при раскалывании доски для тамэсивари. В связи с этим, в справочной литературе по прочностным характеристикам древесных материалов значения σп, Е, ( а тем более kδ ) при растяжении-сжатии древесины поперек волокон почти не представлены, как не имеющие практического интереса. В виде исключения можно привести лишь найденные в источниках информации /4/ значения предела прочности сосны σп=5,4 МПа и ели σп=5,0 МПа (доски для тамэсивари чаще всего изготавливаются из этих пород деревьев) при растяжении поперек волокон с их радиальной ориентацией. Интересно отметить, что предел прочности сосновой доски с продольным расположением волокон (типичное расположение для балок) достигает при изгибе примерно 80 МПа, а модуль упругости Е составляет порядка 109 Па. Следует отметить также, что для древесины характерен большой разброс прочностных характеристик в зависимости от ее влажности, строения волокон, наличия сучков и пороков.

Чтобы определить значения характеристик σп, Е, kδ для рассматриваемых условий тамэсивари, были проведены специальные экспериментальные исследования, методика и результаты которых представлены ниже в отдельном разделе.

1.2. Динамическое нагружение досок. 

При динамическом (ударном) нагружении досок корректный расчет взаимодействия ударника (ударяющего тела) с объектом (доской) существенно усложняется. Деформации в этом случае носят волновой характер и при больших скоростях соударения могут зависеть от локальных условий взаимодействия в окрестности контакта (контактные явления), соотношения масс и упругих свойств ударника и доски. 

В практике расчета прочности балок при динамических нагрузках используют приближенную (техническую) теорию удара, основанную на эквивалентности прогиба балок при статической и динамической нагрузке. 

В рамках технической теории удара введено понятие динамического коэффициента, позволяющего сопоставить друг с другом на основе разработанных аналитических уравнений условия динамического и статического нагружения. Однако, эти уравнения справедливы только для случаев прогиба доски в рамках упругой деформации (участок 1 на рис.5) и непригодны в их исходном виде для расчетов ударного разрушающего воздействия на доску. 

Для выхода из сложившейся затруднительной ситуации были проведены экспериментальные исследования со статическим и динамическим нагружением одиночных досок, а также с динамическим разрушением стопок (групп) из двух и трех досок. 

2.1. Характеристики разрушения одиночных досок. 

Эксперименты проводились в определенной последовательности. Сначала измерялись разрушающая нагрузка Fр и прогиб досок δ перед разрушением при статическом нагружении. Затем определялась суммарная энергия, затрачиваемая на разрушение досок падающим грузом массой m=2 кг. Для испытаний использовались сосновые доски с влажностью 10-12%, размерами L х b х h = (285±10) мм х 215 мм х 22 мм и массой 620±10 г. Большинство досок имело невыпадающие сучки (от 1 до 5) небольшого размера (до 15 мм в диаметре). В соответствии с правилами соревнований по тамэсивари в виде спорта Киокусинкай размеры стандартных досок должны составлять 330 мм х 210 мм х 24 мм. Разница в размерах использованных в экспериментах и стандартных досок не играет существенной роли, так как формулы, приведенные в разделе 1, позволяют без проблем пересчитывать характеристики разрушения, полученные в данных экспериментах, применительно к доскам другого размера. Расстояние между опорами Lо, на которые укладывались доски, во всех экспериментах было одинаковым и составляло 260 мм.

Статическая нагрузка создавалась с помощью пресса /5/. Средняя величина разрушающей нагрузки при испытании 10 досок составила Fр = 115 кгс (1127 Н)±20%. При принятом выше соотношении разрушающей нагрузки к величине нагрузки на пределе упругости доски Fр/ Fп =1,2 значение Fп = 96 кгс (940 Н). На основании формулы (4) можно рассчитать предел прочности древесины: 

σп = Fп/(2/3)(bh2/Lо) = 940/(2/3)(0,215·0,0222/0,26) = 3,5·106 Па = 3,5 МПа,

(при расчете размерность нагрузки принималась в Ньютонах, размеров доски – в метрах).

Измерение прогиба досок осуществлялось при нагрузке F = 95 кгс (930 Н), т.е. почти на пределе упругости досок. Значение прогиба в этих условиях по результатам 10 испытаний составило δ = 4,7 мм = 4,7·10-3 м ±25%. Используя формулу(5), получим значение модуля упругости древесины: 

Е = FLо3/4 δbh3 = 930·0,263/4·4,7·10-3·0,215·0,0223 = 3,8·108 Па

На пределе упругости доски при Fп = 96 кгс (940 Н) расчетный прогиб доски δп равен 4,8 мм. По уравнению (6) можно определить величину энергии, затрачиваемой на упругий изгиб доски: 

W1 = (1/2) Fп δп = 0,5· 940·4,8·10-3 = 2,2 Дж

Суммарная энергия Wр, необходимая для изгиба и разрушения доски, определялась путем динамических испытаний по минимальной высоте H (или скорости V) падающего груза (масса m = 2 кг), при которой происходило растрескивание доски: 

Wр = mgН = mV2/2     (9)

Согласно результатам экспериментов /5/, минимальная высота Н оказалась равной 0,44 м (V = 2,93 м/с), величина Wр = 8,6 Дж. Величина энергии, приходящаяся на необратимые процессы ударного разрушения древесины: 

W2 = Wр – W1 = 8,6 – 2,2 = 6,4 Дж

Отношение W1/Wр, которое характеризует относительную долю энергии, затраченной на преодоление упругих сил доски, составляет ~25%.

Если работу по динамическому разрушению доски геометрически представить в виде диаграммы, приведенной на рис.5 для статической нагрузки (работа равна суммарной площади участков 1 и 2), тогда с помощью формулы (7) можно вычислить полную деформацию доски 

δр = δп + W2/1,1Fп = 4,8·10-3 + 6,4/1,1·940 = 11,0·10-3 м = 11 мм, 

а также коэффициент относительной деформации 

kδ = δр/δп = 11,0·10-3/4,8·10-3 = 2,3

В общем случае работа при динамическом разрушении доски выше, чем при статическом, так как в первом случае часть энергии затрачивается на ускорение массы доски в процессе ее ударного прогиба. Эти дополнительные затраты энергии в неявном виде отражены в значении коэффициента относительной деформации, знание которого позволяет прогнозировать величину энергии динамического разрушения доски в конкретных рассматриваемых условиях по результатам ее статического нагружения.

Таким образом, для сосновых досок с влажностью 10-12% в результате проведенных исследований получены следующие характеристики: 

- прочность древесины поперек волокон при изгибе σп = 3,5·106 Па,

- модуль упругости древесины Е = 3,8·108 Па, 

- коэффициент относительной деформации kδ = 2,3 

По этим характеристикам на основе приведенных выше формул можно рассчитать для досок подобного типа с другими размерами величину разрушающей нагрузки: 

Fр = 1,2Fп = 0,8(bh2/Lо)σп = 2,8·106(bh2/Lо)     (10), 

(размеры в формуле принимаются в метрах, нагрузка – в Ньютонах); 

деформацию упругого прогиба: 

δп = 0,83FрLо3/4Еbh3 = 5,5·10-10 FрLо3/bh3     (11), 

(нагрузка – в Ньютонах, размеры доски и прогиб – в метрах);

полный прогиб: 

δр = kδ δп = 2,3 δп     (12),

а также энергию динамического разрушения доски: 

Wp = 1,1Fп δп (kδ – 0,54) = 1,6 Fр δп     (13), 

(нагрузка – в Ньютонах, прогиб – в метрах, энергия – в Джоулях).

В приведенной ниже таблице 1 в качестве справочного материала представлены характеристики разрушения досок различного размера, 

рассчитанные по формулам (10)-(13). При расчетах принималось, что расстояние между опорами Lо во всех случаях меньше длины досок L на 15 мм, т.е. «захлест» края досок на опору предполагался равным 7,5 мм.

Можно напомнить, что реальные значения характеристик разрушения могут значительно отличаться (до 20% и даже более) от представленных в таблице только за счет разброса прочностных характеристик древесины досок.

Известна старинная притча об отце многочисленного семейства, призывавшего своих сыновей держаться вместе, чтобы успешно противостоять любым невзгодам. Чтобы убедить сыновей в правоте своих слов, он предложил им сломать метлу, связанную из прутьев. После безуспешных попыток сыновей выполнить эту задачу, отец легко ее решил, разломав ветки метлы по очереди. Доски, собранные в группу, при ударном воздействии также «держаться» друг за друга, что повышает степень их общего противодействия динамическим нагрузкам. Рассмотрим на качественном уровне особенности физических процессов при ударном разрушении групп досок.

Как видно из представленной выше таблицы, полный прогиб одиночных досок при их разрушении не превышает 20 мм. Это означает, что если группу досок сформировать в стопку (с использованием прокладок между ними вдоль опорных краев досок) с промежутками 20 мм и более, то при ударе все доски будут разрушаться практически независимо друг от друга. Чтобы обеспечить в этом случае разламывание всех досок, к каждой из них необходимо приложить нагрузку не ниже разрушающей для одной доски (Fр), а общая затраченная энергия (WN) должна быть равна сумме энергий разрушения отдельных досок WN = NWp, где N – количество досок в группе. При таком расположении досок разрушение происходит с минимальными затратами энергии и минимальными нагрузками.

Другой предельный гипотетический случай с максимальными затратами энергии и с максимальными нагрузками можно представить себе, если предположить, что доски в группе прочно связаны друг с другом, как в монолитном блоке. Разрушающая нагрузка и энергия такого блока возрастут (по отношению к одной доске) пропорционально квадрату толщины блока или квадрату количества досок в группе. В этом случае суммарная энергия разрушения досок WN = N2Wp. Поля нагрузок и энергий для групп досок между этими предельными случаями представляют собой возможный диапазон изменений реальных значений разрушающих характеристик. Чтобы пояснить роль контактных явлений между досками в группе на эти характеристики, рассмотрим схему динамического воздействия на группу из двух досок (рис.6).

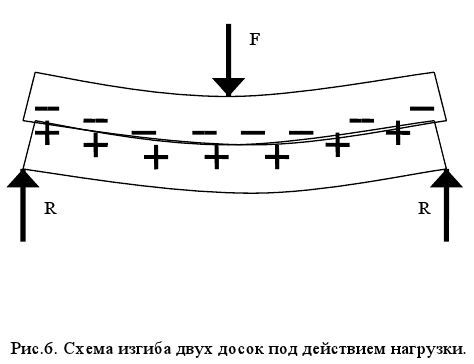
Нижняя поверхность верхней доски при изгибе удлиняется под действием сил растяжения (см. рис.3). Верхняя поверхность нижней доски, наоборот, укорачивается под действием сил сжатия. Силы трения между этими двумя поверхностями препятствуют их смещению относительно друг друга, снижая напряжения растяжения-сжатия и повышая, таким образом, стойкость досок к воздействию ударной нагрузки. Можно ожидать, что отмеченный эффект повышения прочности группы досок должен возрасти, если группа будет состоять из трех (или еще большего количества) досок за счет увеличения числа контактирующих поверхностей. Простых аналитических методов корректного расчета прочности групп досок в условиях ударных нагрузок не существует, поэтому целесообразным представляется проведение экспериментальных исследований. 

Эксперименты по раскалыванию одной и двух досок с размерами 285х215х22 мм (расстояние между опорами 260 мм) падающим грузам с массой 2 кг уже проводились авторами ранее /5/. Было установлено, что энергия разрушения двух досок лишь на незначительную величину превышает удвоенное значение энергии разрушения одной доски. В дополнение к этим экспериментам были поставлены опыты с использованием досок из этой же партии по ударному раскалыванию групп из трех досок. В таблице 2 представлены: экспериментальные значения энергии разрушения одной, групп из двух и трех досок, расчетные значения энергий при их независимом разрушении, а также энергия разрушения одиночного монолитного блока с толщиной, равной суммарной толщине досок в группе.

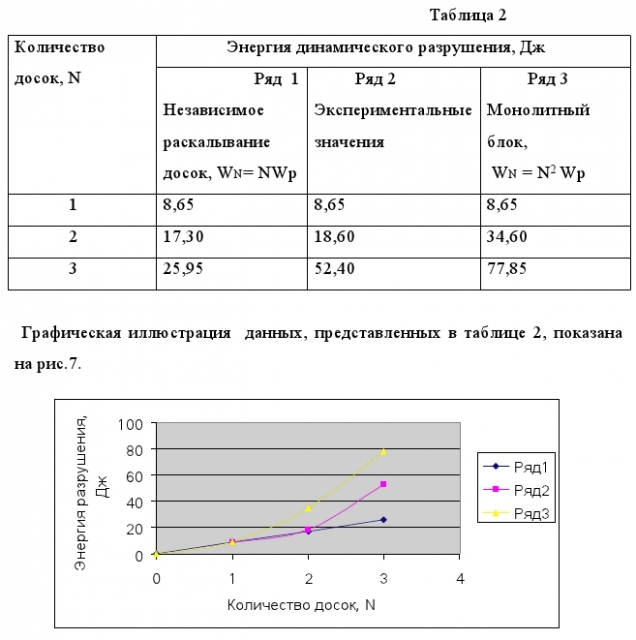
Как следует из результатов исследований, энергия динамического разрушения группы из двух досок примерно на 10% превышает сумму энергий разрушения двух одиночных досок. При переходе к группе из трех досок зафиксировано резкое повышение относительной прочности досок при ударном воздействии. Энергия разрушения такой группы в два раза выше суммы энергий разрушения трех одиночных досок, что соответствует общей энергии разрушения шести одиночных досок. 

Результаты экспериментов качественно согласуются с рассмотренными выше физическими процессами динамического разрушения групп досок. Приведенные выше конкретные количественные значения характеристик разрушения досок получены при ограниченной статистической выборке и их следует рассматривать, как предварительные. Они нуждаются в дальнейшей проверке и уточнении, при этом немаловажным может быть и совершенствование методики испытаний. В частности, результаты динамических испытаний могут зависеть от характеристик ударника – его массы, формы, плотности, упругих свойств. Представляет интерес также исследование ударной прочности групп досок с более высоким количеством.

У любителей легкой жизни может возникнуть искушение повысить результаты в тамэсивари за счет искусственного снижения трения между контактирующими поверхностями досок в группе - проще всего этого можно добиться, например, натерев поверхности куском мыла. Авторы надеются, что настоящие специалисты по тамэсивари выберут другой путь – повышения эффективности своих ударов. 

Оценка потенциальных возможностей использования ударной техники для расколачивания досок может быть предметом последующих публикаций. 

- Джек Хиббард. Искусство каратэ. Техника разбивания предметов и ее практическая ценность в самозащите. - М.: АСТ·Астрель, 2008. 

- В.Н. Попенко. Техника сокрушительных ударов - М.: АСТ·Астрель, 2011. 

- Тимошенко С.П. Сопротивление материалов. В 2.х томах.-М.: Наука, 1965. 

- Прочность древесины. Лесная энциклопедия. Т.2. Сов. Энциклопедия, 1986

- Б.И. Бахтин, Б.Н. Маневич, Д.С. Шапошников. Тарировочные испытания досок для тамэсивари. Официальный сайт Московской Федерации Кекусинкай (МФК), 2010.

- Фотографии 2011.04.03. Чемпионат России по Кекусинкай. Официальный сайт МФК.